PurelyFunctional.tv Newsletter 355: Tip: memoize to trade space for time

Issue 355 - December 09, 2019 · Archives · Subscribe

Clojure Tip 💡

memoize to trade space for speed

In the last issue, part of the bonus of the challenge was to use memoization to speed up the straightforward recursive solution. This is a common use case for memoization.

Take, for example, an implementation of Fibonacci that is a direct translation of the mathematical definition.

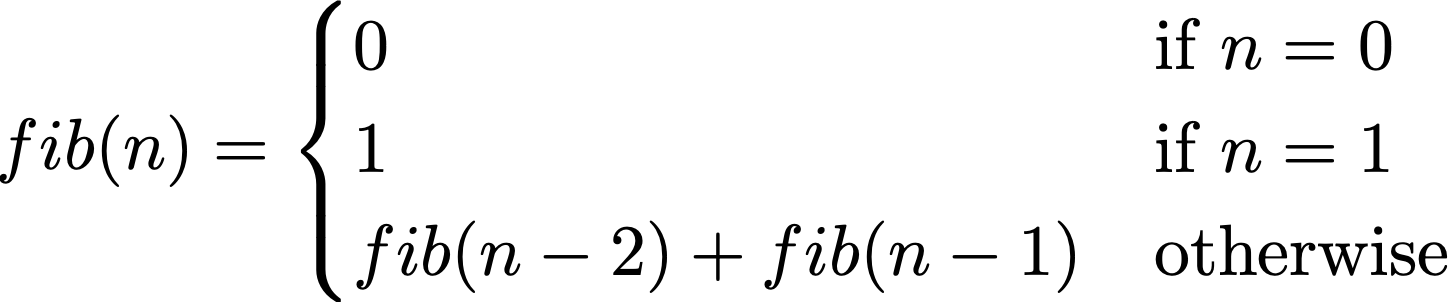
(defn fib [n]
  (cond
    (= 0 n) 0
    (= 1 n) 1
    :else   (+' (fib (- n 2)) (fib (- n 1)))))

Try to run that function, however, on anything bigger than n=10 and it takes much longer than you would think. Why? Because it is calculating the same numbers over and over.

When you call (fib 50), that will have to calculate (+ (fib 8) (fib 9)). But (fib 9) also has to calculate (fib 8)! There's quite a lot of duplication.

We could change the approach and build up the answer starting at the beginning. That would solve this problem and be very fast. But that's hard to read. You lose the natural translation from the mathematical formula.

Another solution is to find a way to store the answer the first time you calculated it so that the next time you need it, you just look it up. That's where memoization comes from.

Memoization basically means wrapping a function with another function. That wrapper function will cache the answers and the next time you pass the same arguments, it will return the cached answer. If you apply it to fib above, it will run fast again, yet the code still reflects the mathematical formula.

The Levenshtein distance in the challenge last week had the same problem as Fibonacci. It has a nice, succinct, recursive definition.

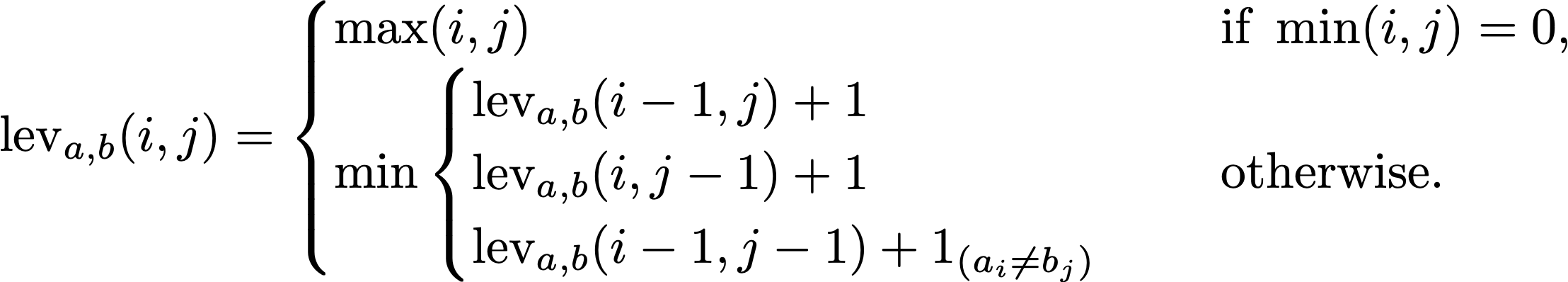
lev is called recursively and things are recalculated many times. Calling this function on long strings will be slow. The answer is to memoize it. You use space to store the calculated answers, but save time since you don't have to re-calculate.

If you're interested in how to implement memoization, I have a podcast episode about it. Clojure comes with a function called memoize and there is also a more feature-rich, configurable and extensible library.

Next week, I'll go deeper into memoization and its limitations.

Awesome book 📖

The Timeliness Way of Building

Whenever I need inspiration about the creative process, I pick up this book. The premise is that Christopher Alexander, a mathematician and architect, was trying to find a way to tap into our deep intuitions about how to build. The language touches the mystical. For me, it has a unique way of reminding me of all of the things that are important that are often overlooked when following strict process. The aim is to imagine and build something that helps humans thrive, which is something I aspire to.

Book update 📖

Chapter 5 is out! Buy it now: Grokking Simplicity.

I'm currently working on Chapter 7, which is all about Stratified Design. There is so much to say. It's a hard chapter because it's all about design, which takes years of experience to develop a sense for. If someone has the experience, what I say will seem obvious. If they don't have the experience, it will seem arbitrary. How can I condense the experience into the pages so that the reader can see what I am talking about?

You can buy the book and use the coupon code TSSIMPLICITY for 50% off.

Clojure Challenge 🤔

Last week's challenge

The challenge in Issue 354 was to implement the Levenshtein distance. Here are the submissions.

This week's challenge

A-Star Algorithm

A neat algorithm for finding a short path through a graph is A-Star. It's used in a lot of games for the characters to find paths through a map.

One thing that's fun about this algorithm is that it's traditionally formulated in terms of mutable data structures. What would this look like as a functional implementation?

Your task is to implement A-Star in Clojure. You can use mutable state if you want! The Wikipedia page has a good description of the algorithm.

As usual, please reply to this email and let me know what you tried. I'll collect them up and share them in the next issue. If you don't want me to share your submission, let me know.

Rock on!
Eric Normand