Tap Into Your Social Brain
Let's look at this logic problem:
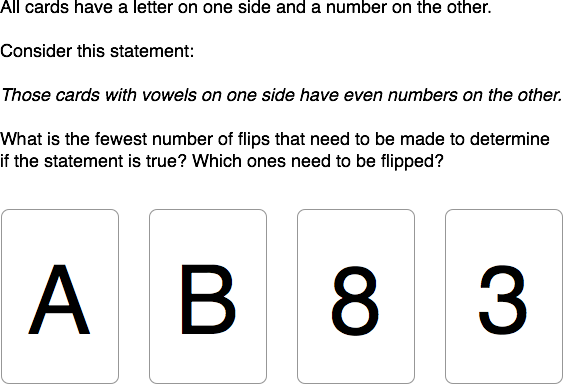
Try to determine the answer.
Hint: It's presented visually to try to trick you (as we saw last time).
The answer is two cards, the A and the 3.
Try this one:
You are a police officer enforcing this law:
It is only legal for minors to drink non-alcoholic beverages.
You are busy, so you need to quickly assess each bar with the minimum amount of checks.
You walk into a bar, and you see this scene:
There are four people in the bar. One is a teenage boy, but you can't see his drink. One is an old man, and you can't see his drink. The third person has a coke^1, but he/she is behind a column so you can't see their age. The last person has a big pint of beer, but he/she is also blocked by a column.
Did you get the answer? You need to check two people. You don't need to check the old man, he's obviously not a minor. You don't need to check the person with a coke, even though he might be underage. That leaves the other two. The teenage boy on the left might have an alcoholic drink (which you can't see), and the person you can't see has a beer, so he/she might be a minor.
Was that easier? Would it surprise you if I told you that the card problem and the bar problem are equivalent?^2 Why is it easier to solve the bar problem with almost no effort?
There are two reasons: one, it calls on years of built-up, real-world experience. Second, the problem is social---that is, it is about people. We humans are built to handle complex relationships between people. Our reasoning power is somehow magnified and clarified when phrased in terms of people in a familiar situation.
Moral: When possible present a logic problem as a problem people have no difficulty solving.
What's interesting is that you instantly know the shape of the solution when presented with the bar version of the problem. You think "I'm looking for minors and alcoholic beverages." Whereas my first reaction to the card version was "I'm looking for vowels and even numbers" (which is wrong). Only after careful, slow, deliberate thinking was I able to see that I should be looking for vowels and odds.
If you present material in the right way, it will help you teach the material better. You've likely had this experience before. Did your teacher ever do a math problem in terms of buying something and making change? Somehow, kids who score poorly in math class can still do the same problem when it's presented as a human-to-human exchange!
Social problems are not the only ones that we are hyper-capable of solving. There are also other situations that we are hardwired to understand better than symbolic puzzles. Spatial orientation (for instance, that the arm sticking out from behind the column is attached to a person) and movement are also easy to solve, and luckily some of the most interesting math problems are equivalent to orientation and motion.
By converting a symbolic problem to one that is a familiar, real-world situation, you are tapping into many different parts of the brain. The key to a good logic-to-social conversion is whether the problem solver can properly simulate the situation themselves. The bar problem is good because it's something we can all imagine.
This is one thing I try to take advantage of in my videos. Yes, you are learning Clojure to solve a very complex problem. However, the problem is familiar to most, as it involves many metaphors and simulated situations. You are teaching someone to bake. A function is like a recipe. Pure functions are like doing a calculation in your head. Side effects move you around or use up ingredients, etc. I worked hard to make it seamless to learn.
Now that we know that it's easier to learn something if we can already simulate it, the next question is how to convert math/logic problems from their symbolic form into something more suitable for whole-brain simulation. This post is long enough already, so I'll address that next time.
- Yes, I come from that part of the country.
- Here's the conversion: minors are vowels, legal-aged are consonants. Alcoholic drinks are odd numbers, non-alcoholic drinks are even numbers. And legal is true and illegal is false. (That is the big one!)