Eric Normand Newsletter 469: Everything is a center
Reflections 🤔
Everything is a center
I learned functional programming hand-in-hand with unlearning object-oriented programming. And in doing those things, I learned to express ideas more directly and more powerfully.
But yesterday, while getting a lesson in OOP and moldable
development
with Tudor Gîrba and Gene Kim, I was appalled by Tudor's use of object
references. He modeled a Ludo game with classes like Game, Square,
Token, and Player. The Game had references to Squares. And
Squares had references back to the Game they were in, modeling
reciprocal relationships with two pointers.
These kinds of models bug me. They remind me of my days of Java programming---the very stuff I uprooted to find better ways to express myself in FP.
But Tudor and his peers have created cool stuff with Glamorous Toolkit. So I suppressed my distaste as best I could to try to learn what he was teaching.
We discussed these issues at length during the lesson. I don't know how well I expressed it during our call, but my issue with this kind of modeling is that it tends to obscure the actual problem. For instance, the problem of board game software is to:
- Visualize the board for the players.
- Determine which moves are valid.
- Calculate the effect of a given move.
All three of these concerns require top-down knowledge of the entire board state. There's no point in creating a class to represent a particular square on the board when its name should do. You can always say "the third square from the start position" to identify that square. Why make a class (with state and behavior)?
A similar modeling problem comes up in the Student-Course registration
problem
(students enroll in multiple courses, and many students are in each
course). In classical Object-Oriented Analysis and Design (OOAD), you
make a class Student and a class Course and have to maintain
reciprocal relationships using references. But it misses the actual
problem: that of recording a many-to-many relationship. If you're going
to make a class, make a ManyToMany class. In other words, don't
simulate students and courses. Simulate the registry---the physical book
schools used to use.
A similar problem with OOAD comes up in Conway's Game of Life. The
classical approach makes a Cell class (which knows whether it's dead
or alive) and a Board class (which knows all the cells). All sorts of
problems come up. The worst issue is that you need to freeze the state
to calculate the next state since each turn happens atomically (at the
top level!). But what the OOAD approach misses is that calculating the
next turn is about counting live neighbors, not about laying out a
board. Once you look at it that way, you get the crazy-terse APL
one-liner
(here
translated to Clojure).
It would help to look for those concerns first. The concerns then inform
the representation. OOAD obscures the concerns behind false, incidental
concerns. You worry about where to store the state for dead/alive (it's
a property of a cell, so you need a Cell class, etc.). State is an
incidental concern. The problem never mentions it.
I tried to express this to Tudor, and he had an answer: What about the concerns of exploring and explaining this stuff? I know how to pick apart the use cases for a board game because I have programmed board games before. I have already figured it out. But what if it was new to me? Where do I start? I came up with representing the student registry only after thoroughly exploring the problem and encountering multiple dead ends. In truth, I don't know if I could ever come up with the APL Game of Life solution myself.
What about the concern of explaining what the software does (or should do) to a non-programmer? Or, put another way, how do I keep explanations in terms native to the problem? The Student-Course problem never mentions many-to-many relationships (a technical term)---and I only presume the existence of a pen-and-paper registration book. And the Game of Life solution (even written in Clojure, a language I love) is just hash maps, vectors, and sets! The code doesn't guide the reader to the epiphany of counting neighbors. A reader has to claw their way there themselves.
Tudor says things I've never heard before: A class gives you something
to visualize. It gives you a place to enforce invariants. (Well, I had
heard that before, but only from other Smalltalkers.) And most
surprising: Every object is a center; you should always be able to reach
out from self to get any information you need (including if it
requires cycles in the object graph) because you don't know what the
"top" is in the top-down view.
This kind of modeling still feels wrong, but I trust that Smalltalk contains a lot of wisdom not found in Java. My sentiments evolved in Java codebases, so they're probably not good guides to Smalltalk models. I'm curious how my modeling approach will unfold as I play more in Smalltalk. Can I improve my FP and (true) OOP simultaneously? How will I express myself after this exploration? And will I still like Clojure? I'm packing my sense of adventure for this mind-bending journey.
Stack Overflow Developer Survey 📋
Stack Overflow does a yearly, global survey of programmers to figure out who's out there. They share their data after it closes. Clojure tends to do very well in terms of developer happiness and income. Please fill out the survey. It will help Clojure make a good showing. The survey has been simplified from previous years. I think it took me 10 minutes.
Grokking Simplicity 📘
It's nice when a biggish name mentions they like my book:
[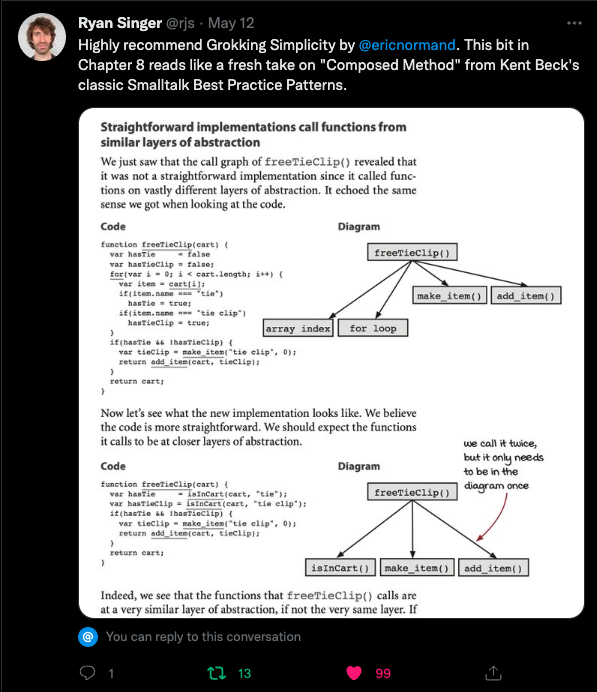](https://twitter.com/rjs/status/1524854532936810501)
You can order the book on Amazon. Please leave a rating and/or review. Reviews are a primary signal that Amazon uses to promote the book. They help others learn whether the book is for them.
You can order the print and/or eBook versions on Manning.com (use TSSIMPLICITY for 50% off).
Clojure Challenge 🤔
Last challenge
Issue 468 - Maxie and Minnie - Submissions
This week's challenge
Lazy Fibonacci Sequence
Ah, the ubiquitous example of recursive functions. Well, this is not your traditional fibonacci sequence exercise.
We all know that the fibonacci sequence is defined as:
(fib 0) ;=> 1
(fib 1) ;=> 1
(fib n) ;=> (+ (fib (dec n)) (fib (dec (dec n))))
And we know we could generate it forward, one element at a time, in a lazy fashion. That is your first task!
(fib-seq) ;=> (1 1 2 3 5 8 13 ....) lazily generated because it's
infinite
But we could parameterize some of the things in the definition, like the
first and second elements (both 1s), and the operation to apply (+).
We should be able to pass them as arguments:
(fib-seq + 1 1) ;=> (1 1 2 3 5 8 13 ....)
That's your second task.
Your third task is more interesting: We don't have to limit ourselves to
addition. In fact, we should be able to use any function that takes two
arguments of type T and returns a value of T (closure property). Your
task is to generate the first 10 elements of the sequence (use take)
for each of these combinations:
(fib-seq str "X" "O")
(fib-seq * 1 1)
(fib-seq * 1 2)
(fib-seq * 1 -1)
(fib-seq vector [] [])
Thanks to this site for the problem idea, where it is rated Expert in Java. The problem has been modified.
Please submit your solutions as comments on this gist.
Rock on!
Eric Normand