Building composable abstractions
Do you want to create robust and composable abstractions? Conal Elliott's Denotational Design is an iterative process to define the essence of a domain and build in composability. The resulting abstractions lead to more robust code at the core of your application and can give your business a competitive advantage. This is the process that created Functional Reactive Programming. We will apply this process to the Quil graphics library to develop a composable vector graphics system.
Slides
Transcript
[So I have this thing on the screen. A little question that just keep in the back of your mind while I'm while the talk is going on. My name is Eric Normand. The title of this talk is ][Building Composable Abstractions.][ You might know me from PurelyFunctional.tv---that's my company. My newsletter used to be called the Clojure Gazette. Please sign up.]

[I often get asked how to make abstractions like take a problem and break it down and turn it into functional code. A lot of people are able to solve small problems like Fibonacci---and that's kind of the typical example you see online. But then when they finally want to create an app, they're stuck. They don't know how to take the tools that they've learned and turn them into software.]
[So that's kind of the the purpose of this talk. To develop a process to do that. And also, I'd like to start a discussion about how we can do that better. Here's sort of the map of the talk. Why focus on abstractions? We're going to talk about the process. And then go through a pretty in-depth example app or at an example abstraction and go through the process with it. And then we'll conclude with some like feel-good stuff.]

[So I first have to motivate why abstractions are important to talk about. I really like this book Refactoring. I love the book. It's really great. It defined refactoring which is now like a common everyday word. Like this changing software systems in such a way that it does not alter the external behavior of the code. Now the thing I like about this is it in the general industry, we now have this idea that there's a difference between the behavior of the code and the actual implementation. The actual code itself.]
[I really credit it for that. But the thing is, it's not enough. Because what happens when people do refactoring is, they think I can just code it and then clean it up. I can just start coding and later I'll make it better. So let me explain that a little more why you can't always make it better.]

[This is Isaac Newton. He developed a system called Newtonian Mechanics. It's three really elegant laws and this system is the prototype of mathematically based scientific systems. It's what everything aspires to and there's actually four really simple concepts in it. And if you use these, you can say anything in Newtonian mechanics.]

[Now this replaced Aristotelian physics. That was the system that people thought was the truth about how the universe works for thousands of years. And in this system, you have these. This is just a subset of the concepts. You have a concept like ideal speed. Ideal speed is basically saying small things move faster than big things. And natural place says rocks sink to the bottom of the water so that's its natural place. And it just stops there because that's where it wants to be. And then you have water that sits on top and that's where it wants to be. ][like why doesn't the air go into the water? well, it's natural place is on top of the water.]
[Natural motion oh! That's when you're doing smooth easy motion like that is generated by the thing itself. And then unnatural motion that's when you get jostled, right? That's unnatural. So you can kind of see how this might have developed. Like a student would ask Aristotle like: well why is it that I can throw a little rock really far and fast but a big rock I can't even get it very far? And he's like oh! Well that's called ideal speed. Big things just move slower than small things.]
[And then the student has another user story. Well natural place: why is it that rocks fall to the bottom of the ocean? Oh that's just called natural place and so he comes up with a little answer to that user story. And then natural motion. Another user story. So just view one user story at a time.]
[This system of physics has aggregated into something that you can kind of see. It's just a big mess, especially if you know Newtonian mechanics. It's much cleaner and elegant so the thing is you can't refactor Aristotle into Newton. There's no way to change from this system with these concepts. Like ideal speed into velocity and acceleration. There's no way to do it. ]

[So I put a tweet icon up there. The reason is I like it when people tweet quotes from a conference talk. And so I'm helping you out. I've measured them. They're ready to be tweeted.]

[Alright. So Newton---he's a really good example. That's why I kept him in the talk even though I might go long. He had this quote: "If I've seen further it's by standing on the shoulders of giants".]
[There's three interpretations. One is he was a humble person—which is not true. So we can rule that out. Number two was he was insulting his rival who was a short man. It wasn't him. It was a giant that I was standing on. Okay. That's probably true but I actually prefer the third interpretation which is he's giving us a method. He's telling us how he did, what he did, all you have to do is read and learn from people in the past. What they've done? What they did wrong? What they did right? How they did it? And you just have to see just a little bit more than what they saw and you'll do something great because no one else is doing that thing. And everyone will be impressed so there's a little visual thing.]
[The thing is, over time we've added so much knowledge since his time. So if we graph this well, he had to invent calculus. I don't know if you knew that. We all actually have calculus for free. He had to spend years developing the notation and everything. So if you graph this giant height over time, there's Newton over there and we're like almost at the Asymptote.]

[We got so many people. So many giants stacked on top of each other that we're able to see way farther, way faster. My teacher always told me to label my graphs.]
[So we actually can write something like Newtonian mechanics every day. It's three equations. We can do that on a computer. Not only that, but we can actually run the thing. We can do more calculations than Newton did in his whole lifetime in minutes and see if it works.]
[The cool thing is that because we have computers, we have access to all the knowledge—more than knowledge than he had. Access to giant height is higher but we also have a system programming which encourages us to make Newtonian-style systems instead of Aristotelian systems. Who uses an Aristotelian system at work where it feels like it's just a bunch of big ball of mud—spaghetti code? Don't you hate it? Don't you wish you would be able to write something more clean and elegant?]
[So there's another tweet. Alright. So where does that Refactoring book come in? Well, we're gonna come back to that but I just want to say that cleaning up is really important and I'm glad that we have this idea. But it's like talking about cleaning up your room. It's really therapeutic. It's important. It helps you be more productive and everything. But then, it doesn't tell you like what needs to be in your room? Why do you have a room? What what does your room have to be like?]

[Okay so I've developed a process and here are the objectives for that process. It has to consistently produce good abstractions and by good abstractions, I mean the Newtonian type. So there are gonna be better and worse abstractions that you know have better properties and worse properties for your particular problem. But this produces Newtonian style and it's an iterative process. So it's gonna get you something. You might not like it but you can learn from making it. How to make it better. Right. You make it. You learn something, you revisit your design decisions, you start again. Anyone can do it.]
[What I mean by this is you can do it from stuff you already know. Like you don't have to go study an abstract branch of mathematics to be able to do it. You can start with what you've got right now. And then fosters collaboration. This is really important. We work on teams now and so we need to be able to talk about what we're doing. And so often I find that I've like just invented a new concept. It's like a new abstraction and I can't talk about it and I try and it just confuses people. And so we have disagreements about different things. Like we're not even talking about the same thing. So I feel like this is a way to solve that. There's a way to solve this and this is actually one of the easier problems to solve. ]

[This talk was and the process was largely inspired by Conal Elliott's Denotational Design and in the abstract I said I would be teaching that. But I realized that my objectives were much different from his so I kind of went in a different direction. So I apologize if that's what you wanted to learn. It is very worth learning. It's very cool stuff but mine is cool too so I don't feel that bad.]
[Ok an example. This is the example. We're going to develop vector graphics system and we're gonna use the process. It's a very simple vector graphic system so we can go through it quickly. But if someone said we're gonna do a vector graphic system in Clojure, I think quill and it's true. It's a vector graphic system but it doesn't do what I want.]
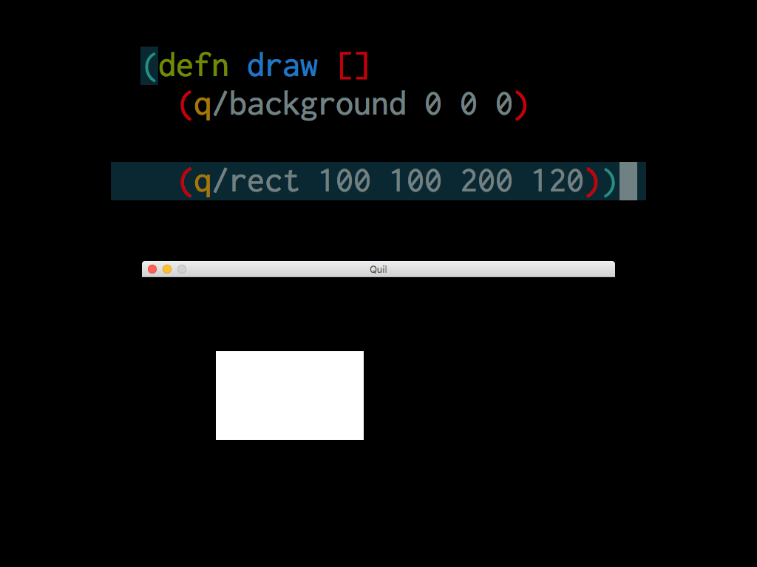
[So let's see a little bit how it doesn't do exactly what I want it to do. So here's a simple quill thing. We do a background and it just makes the window all black. If I want to draw a rectangle, I have to do rect give it an XY coordinate and within a height. If I want to make it red, I put fill before I draw so it's kind of like I'm dipping a pen in the paint and so like the last paint color I dipped in. A paint brush in paint. The last color I dip it in, that's the color whatever I'm gonna draw next.]
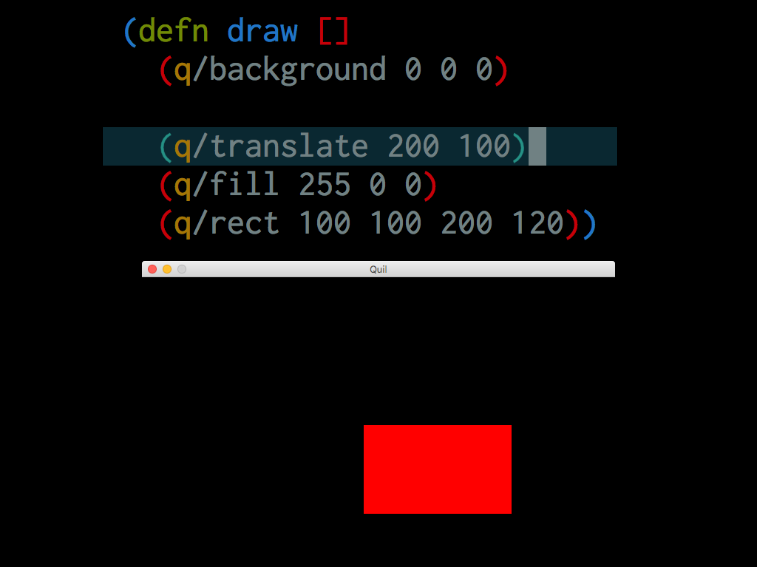
[Translate. So I can move the rectangle by putting translate before I draw. Okay. So it's kind of like saying well, I'm gonna move my arm over and then draw right? Okay now we're gonna get to some problems. If I do rotate and I put it before the translate, it doesn't just rotate the rectangle where it's at. It actually is like rotating around the the top left of the window and so it's it's almost like I have to move. And then I turn right or I turn first and then I moved from wherever I'm at right?]
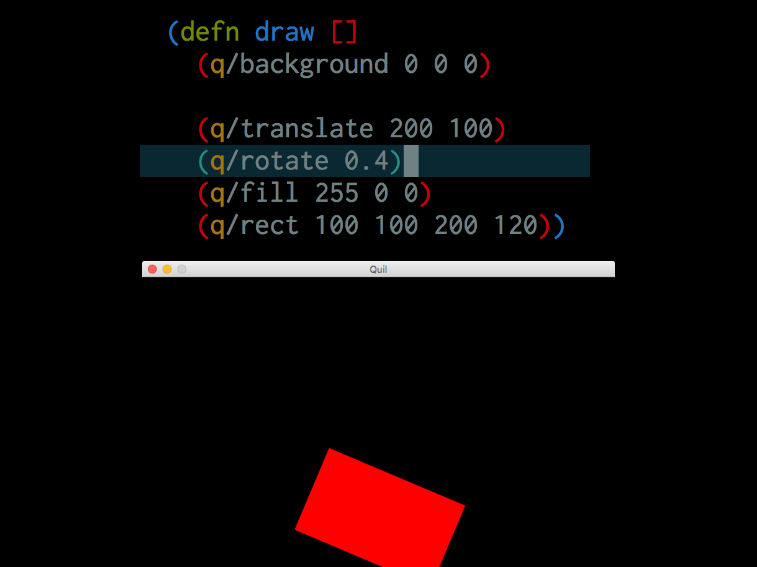
[And then I draw but if I put rotate after translate, it does rotate in place around the the top-left corner of the rectangle. So it's like I step. So I'm translating so I step over and then I rotate and then I draw. So, this isn't how I draw. It's kind of counterintuitive to me. It does have a very formal mathematical basis. It's called affine transformations but it's not what I want.]

[Okay. So now we're gonna go through the steps. Three steps. Physical metaphor meaning construction and implementation. I'm gonna go through each of the steps. Well basically what we're doing is hammock time. We are in two steps before I even start implementing. But this is what this is thinking if someone says just think about it first. Well we don't know what to think. It's indistinguishable from procrastination but this is a formal process that actually gives you stuff along the way so you know you're making progress.]
[Alright so the Physical Metaphor. The idea behind this is to choose a metaphor that will capture the important information in your program and this can actually become the first implementation of your abstraction. So you already start with an existing implementation before you've written any code. And also, because it's physical, we live in the physical world since we were born. So like we're really good at answering questions about the physical world. We'll see that.]
[Alright. So it has the good metaphor to be able to answer questions and it has to be a shared experience. Another thing is, we can talk about our physical experience. Alright! So let's go through some examples of what we could use for vector graphics. Could be painting---which we saw. But maybe we have a better metaphor than the one where you're moving around and drawing stencils clay projected light. All of these are good metaphors and they answer the questions. So if I want to put a green square on top of a red square, what happens? Well if we're painting, it means that the red and the green are gonna mix a little when they overlap. But if we're doing clay well, the clay is gonna like sit on top and so you'll see the one on top and not the one on bottom.]
[So see! It answers the questions right? And I would like to stress that the particulars of the vector graphic system that I'm developing, they're not that important. But you should be seeing the process and the thought process that's what I'm trying to express. So there's these are all good metaphors but they have different answers to the questions. So what are we gonna choose? Shapes in construction paper. So just to elaborate the metaphor a little bit, I have different colored papers and some scissors and I cut out shapes like rectangles and ellipses---those are the two shapes we're gonna do.]
[And then, I can move them around and put them like let's say I have a big black piece of paper and I just move them around and put them where I want. And then that's my graphic. So the nice thing is I could explain that in pretty shortly short amount of time. Now you understand it and you can follow along. That's the idea. We're working as a team right now. Now you might disagree with some of the answers that I come up with from my intuition. But at least we're disagreeing about the same thing right? So easy to disagree about two different things and you don't get anywhere.]
[Another question. You could ask if it's not so obvious like kind of a prompt is, how would you do it without a computer? How would you do it before computers existed? And very often it just means you'd do it like pen and paper right? And so you'd have some system like well, I would draw a line down the middle of the page and I'd draw some columns and some rows and I'd put the ID on the left. And then, the name on the right you know you'd have some system and kind of developing an algorithm that a person would follow. ]
[And so I want to say like if you don't think that your abstraction has a metaphor, I've never met a good abstraction that didn't have a good metaphor. I've met some Aristotelian type systems that I just couldn't figure out like what they were supposed to really do. So maybe you don't have a good abstraction. You know if you already have a spec and it's already a mess. Sorry but you might be able to find smaller abstractions within it.]

[Okay so this is a summary of the first step. We have this rich physical intuition. It's how there are studies showing that mathematicians use physical intuition more than notation to do their thinking. And so we can do that same thing. They contain the answers to our questions. We don't have to like just experimenting with different things in code. We can ask our thing and we're gonna see that in the next step, they keep you grounded.]
[Like one thing that happens to me a lot when I start abstracting is I make abstractions that I think might be useful. But there's no real basis in the actual thing I'm implementing. Like just making it overly complex and this grounding you can always just say well what is that in the physical world? Why are you developing that? Like what does it correspond to? Keeps you grounded? And then there discussable.]
[Alright! Second step. This is where you take the intuition you have. You ask yourself questions and you mind it for the answers and you turn them into precise mathematical language. So we're gonna be focusing on the interface right now. The interface is the meaning of the thing. What does it mean to call this method? What does it mean to hit that API endpoint? What does it mean to have an object of this type? We're not saying how the object is implemented. We just know that the type has some kind of meaning.]

[So we need to figure out what are the things in the interface that we want to keep and what's just an implementation detail. We already have an implementation remember? We already have construction paper. What's important about this that we want to keep. So here's a list of things that I'm gonna keep and we'll go over each of them.]

[Okay. So you notice I said precise mathematical language and now I'm showing you a Clojure code. Lambda calculus is math. A subset of Clojure is Lambda calculus. So we can just use Clojure notation to represent our math. Also either there spec on here and spec is fairly well defined mathematically, I'm not a mathematician so I can't say it's perfectly well defined. But I feel like there's an easy subset that you can see like makes a lot of sense and is well defined.]
[So we're defining two types here. Cut out and shape. We're defining a function. We're not implementing it yet and we're saying at the bottom it takes a cut out and it returns a shape. So this is our accessor. We can see what shape something is.]

[We can consruct shapes. So we have the type called color. Not saying what it is yet. Not implementing it and we have a function called rect that will return what I cut out. Takes a color width and height. Same for ellipse.]

[Now preservation of shape. What I mean by this is I can imagine like getting mixed up in quill and doing some weird transformation where now my rectangle isn't a rectangle anymore. You know I don't trust myself to not get into that mess. So what I'm saying is, if I translate it, if I move it around, it's not gonna change the shape. So I've done that by making the spec say that the shape of the return value is the shape of the argument. I pass it and I'm doing the same for rotation.]

[Now preservation of color is very similar. The color of the return value is the color of the argument. Now this is just me covering my bases because I don't trust myself when I'm implementing it. This is like TDD ]

[Overlay order. So I want to be able to put something on top of something else. Just like construction paper and so I'm making a function called overlay. It takes two cutouts and it returns a new cutout.]
[But then, I hope you're all seeing that this is a corner case because I said that all cutouts have a shape and a color. What is it? What's the color of a green rectangle on top of a red rectangle? It doesn't make sense. It doesn't even make sense to ask it. So that's a corner case and you want to avoid corner cases especially at this stage. Like it's really early if you can eliminate the corner case. It's gonna save you a lot of time. Why do you want to eliminate corner cases? We're talking about making stuff that's composable. Composable abstractions. So if you have a corner case, the best case scenario is there's two branches. Two branches in your corner case because it's like an if statement.]
[So if you compose two if statements, you now have four branches. They multiply if you compose again with another one. Another corner case. Now you have eight branches. You compose it again. You have sixteen branches. Now you have a thing that came from one of those sixteen branches. Which one did it come from? Well now you have to query the value itself to kind of figure out. In another if statement, which branch it comes from? This is how this is how messes happen and it's why we feel that some things some api's are not composable. So avoid them like the plague. You don't want corner cases especially this early.]

[So we're gonna redo overlay. I'm gonna find a new type called a collage. A collage is now a collection of things. Put on top of each other. Think the collection of cutouts and we have an overlay that takes a collage in a cutout. So the collage will start empty and we'll add cutouts to it like a like of a reduction. Now we can define a test check property like a mathematical expression of what how it's supposed to behave. And we're basically saying for all cutouts and two different. ][i'm sorry for all collages and two different cutouts. if i put a and then b, it's different from putting b and then a so i'm saying the order matters. ]

[Okay. Rotation and translation independence. What I mean is you saw before, if I translate and then rotate it, it draws a different picture from rotating translate and I don't want that to happen. So I'm going to constrain my system here. So I'm saying if I translate and then rotate, it's equal to rotating and then translating. I'm just saying that as a constraint on my system, rotation is additive.]
[Alright. So if I have a rectangle and I rotate it A and then B, it's the same as rotating at B and then A right? That makes sense. So I'm just expressing that in precise mathematical notation. Same for translation. ]

[If I move it this way and then that way, is the same as moving it that way and then that way. And so at this point, I've been composing stuff together and you notice that I've been defining how the composition works before I've even said how the things are implemented and what they are.]
[So that's how that's kind of like the secret for making things composable as you start with the composition. Before, you've even defined how the thing will draw and we often do it the other way. We're like oh! When I see a rectangle on the screen, so we draw it and then we haven't thought about composition yet. Alright. ]

[So we forgot to draw. So I just have a function that will draw a thing and the thing can either be a collage or a cutout just using spec.]
[Okay so I got to this point and I realized I was very unsatisfied with all of this. I just made you walk through it with me. The reason I'm unsatisfied is like so we did like a kind of a TDD approach. Everything we did was writing tests spec. ]
[We'll do tests, we did test check properties. And so we've defined all of the properties from the outside. And we have all of the work ahead of us. Actually like implementing this thing that's one approach is to have a lot of safety and all the tests. But the other approach is to construct the meaning from pre-existing parts from pre-existing constructs in the language.]

[And what do I mean by that? I said rotation is additive. Well what if I want something that says that if I rotate A and then B, is the same as rotating B and then A. It's just addition over numbers. It already does that and that numbers in addition. Already have that property and like almost nothing else. So we can just use addition with numbers so all we have to do is find constructs that have exactly the properties that we want in our in our meaning.]

[So let's go back. Let's throw it all away and start again. So color. I'm just gonna bottom out on a tuple of integers. I really don't have anything special to say about color so I'm just gonna use the thing. That everyone uses RGB but the interesting thing is that, we're now defining a cutout as a function. Two reasons functions are turing-complete. So you're never like throwing you're never like gonna get into a corner by using functions.]
[The second thing is they have this nice property. That the things that change about functions are the arguments. So if I don't put something in the argument list, I know it won't change and we had this with two things that we want to preserve. Preservation of color and preservation of shape. And now by not putting shape and color in the argument list, I'm guaranteeing that they won't change. So now that whole thing is taken cared of, for me I don't have to have an accessor so that I can test it. You still can if you want but you don't have to.]
[Alright. So two things I want to point out. Meanings have to bottom out somewhere and if you're bottoming out in a well-defined mathematical thing, you're fine. And then you want to choose meanings that have the same structure right? Choose meanings, choose constructs to express your meanings that have the same structure that of the thing you're looking for.]

[Okay. So now here's our constructor for a rectangle. Notice it returns a function of three arguments. Like I said it, cutout is now a function of three arguments. And also notice that there's some quill in there. Well quill is a well defined system so I'm bottoming out on quill. Doesn't mean like I'm stuck on quill. This is just meaning it's not implementation. I just want to say it's acting like this quill code. So notice I don't have color and width and height in the in the arguments of the inner function so I know they're not going to change.]

[Okay. Now it's starting to get interesting. Translate takes a cutout and an X and a Y. And then it returns a cutout so a function of three arguments and it just adds the T X's and the T Y's. So I'm saying that it's additive. That's basically vector addition and it's gonna call the cutout that you passed it with this new translation.]

[Rotation is very similar. Rotation is additive so we're doing the R in our prime. Adding them up and just calling the thing with a new rotation.]

[And overlay. So it takes two cutouts. We don't have a collage anymore. Takes two cutouts and we're using the property that the thing you draw a ][second in quill shows up on top. so i'm drawing a and then b. b is gonna show up on top and i'm just passing in the translation in the rotation. ]

[And now we can define draw as just all the cutout at the origin with zero rotation. It's all zeros now. The reason I like this approach is we can now run it. ]
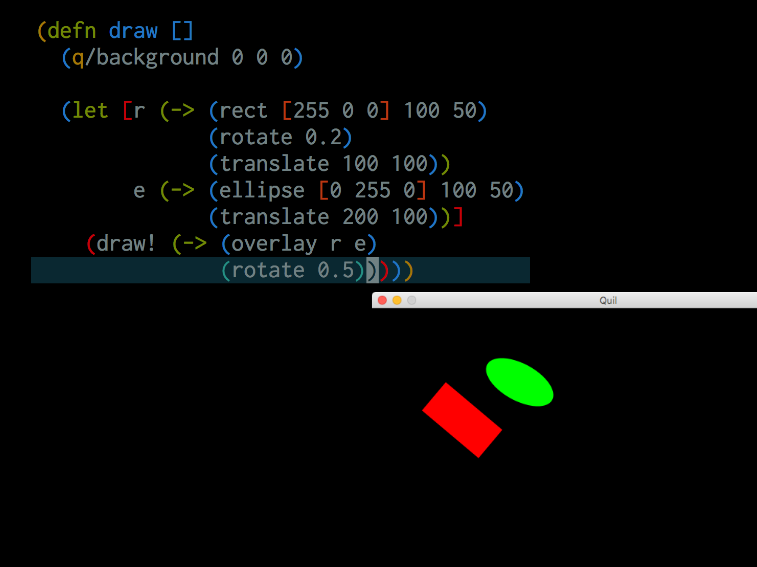
[So I make a rectangle, I rotate and translate it. Make an ellipse and translate it. And then I overlay the ellipse on top of the rectangle and I can see what it does. ][this is nice. it's what i want. then i was playing around with it. i won't show you all of them but i found one that didn't do what i wanted. if i take that overlay and i rotate it, the two things separate now. this because i've developed the physical metaphor. i see this is not what i wanted to do. i know that.]
[Okay. This boom. My intuition is like whoa something's wrong. They're separated out. I thought when I thought rotation of an overlay it's sort of like I grabbed both of them with my hand. And I rotate them together and so they're not gonna move relative to each other but they did! They separated. And so I went back to the code and I saw, oh! I see what's happening. It's like I grabbed both of them independently and turn them. I'm passing to both so they're separate. They're still separate even though they're now being drawn in the same function. It's like I'm grabbing both and turning them.]
[So what do I do? Well I was thinking about it. You know, there's got to be something missing that is in my physical metaphor that I'm not putting in my code. And the thing is, when I when I grab the things, I get to choose where I grab them right? I get to put my hand here. I get to put my hand here and then when I rotate them, it's around the center point. Like around my wrist right?]
[Where my wrist is? So I didn't include that. I didn't include where to grab it. So I want to say that like you have to revisit your physical metaphor. It has the answers. If it's a good metaphor, it has the answer like my first instinct. As a you know, an experienced programmer with bad habits is to just like start trying things. Did you start trying? Oh! What if I you know do something and transform it a little bit? Like that's wrong. Just go back and think about it some more.]

[Okay. So we're gonna add the CX and CY. So that's the center point that's where I grabbed it. And now it looks a little bit more complicated. But this is because in the affine system, you only rotate around the origin. So what I have to do is I grab the things. I move them up to the origin, rotate it and then move it back. And then I can draw them. Okay. So now I have a system. I've made it rotate over time. So R is changing over time and so it's cool! They're rotating and they're not changing relative to each other. I think there might be some distortion on the on the aspect ratio there.]

[Okay. So let's, that's enough of step two to d]emonstrate the process. So let's summarize. You want to preserve the features you want to keep. That's the interface. Eliminate the features you don't need. That's the implementation details. Remember we haven't implemented anything yet. I know I had code that ran but that was just the meaning I said. It means the same as this code. No corner cases. They're multiplicative. You just don't want them.
[You want to when you're constructing your meaning. You want to use constructs that already have that same structure that you're looking for. And they have to be well-defined. So there's a lot of stuff you know. Some kinds of side effects. You don't want that kind of thing. You don't you want to avoid those non well-defined things. And then focus on composition first before you even define what the thing is.]
[Alright. Step three is Implementation. We have something that runs. So it's kind of actually funny to start talking about it now but what if I don't want to use quill? What if I want to use SVG? I can still do that right? But at this point, we already know what to do. We're a Clojure programmers. That's kind of a joke but it's kind of not. But anyway, actually that's where this goes. Refactoring is if we revisit the definition, you're changing the code without changing the external behavior. We can squint and see external behavior. Well that's another way to say the meaning of the code. So we have the meaning already built.]
[Now all we have to do is change the code so that it does what we want. So for instance, if I want to output SVG, I can simply refactor from quill to SVG. But all of my compositions and stuff---those are already done. If I want to be able to serialize it to disk that might be a like a implementation detail that I need. That wasn't like included in the metaphor while functions can't serialize to disk. So I can refactor it into a data structure DSL if I want to be able to run those tests that I had. I need to have the quality between things and I don't have that with functions. So a data structure DSL also is the answer to that.]

[Alright. I want to revisit my objective to see how well this process works. So consistently produces good abstractions. I think I have a lot of work to do to show that this works all the time. I've used it several times and it's been very useful. The thing that I think might be sort of the thing. Now I won't be able to do by myself is if I can just cause I can do. It doesn't mean I've elaborated all the steps right?]
[I would like to elaborate the steps more. Anyone can do also. Yet to be seen but I think that the steps are pretty pretty easy to do. And then fosters collaboration. I think I have shown this for sure because y'all could follow along with you know me moving my hands around and stuff.]

[Okay just to summarize. So you use a physical metaphor for guidance and grounding. Don't want to go space-cadet on these things when you're constructing the meaning. You want to define the parts and their relationships and how they compose. And you need to use precise mathematical language otherwise you're kind of cheating if you can't actually express the thing that you're doing. Implementation. You just have to refactor to get all the meta properties that aren't part of your metaphor. So these are like the implementation details. Needs to run fast. He's to export to SVG that kind of thing.]

[Some corollaries for this process so for each of the steps, there's kind of like an assumption. So in the first step, you have to know your domain. If you don't know quantum physics, you're not gonna be able to do this for quantum physics. And that's it's kind of like an unfortunate thing but you need to. Implementation. You just have to refactor to get all the meta properties that aren't part of your metaphor. So these are like the implementation details. Needs to run fast. He's to export to SVG that kind of thing.]
[Know your constructs that means you have to know the language and how the parts of your language are behave. And what structures they have so that you can express your meaning in terms of them and know your refactoring. So you have to know how to manipulate your code without actually changing the meaning.]
[I have a page up on my site. Please go there and you can download the slides. There's also links to some very much better talks than this that were inspirations for this talk and for this process. And also, sign up for my newsletter. There's a form at the bottom that you can sign up for. That's it! Thank you!]