A Theory of Functional Programming
We hear two common questions from outside the functional programming community: 'What is functional programming?', and 'Why should I use it?'. I have struggled to find good answers to these questions. In this talk, we will look at the existing definition, and I will present a formulation I've been working on that attempts to answer both of these questions and explain why functional programming is so special.
Video
Video + Slides
Slides
Transcript
Thank you so much. I'm so happy to be invited here to speak. Prague is a beautiful city and I'm glad to see so many people into functional programming. And I've never really done functional programming in Europe so this is pretty cool. I was walking around Prague yesterday, I did not get accosted by any Devils luckily but I did see a St. Nicholas. Ah! There we go!


Okay. So who knows who this is? It's Isaac Newton and one of the most famous things Isaac Newton did was to formulate a theory of mechanics and kinematics. And we all know these three laws of motion that are attributed to Newton.

And the thing about them is they're very clear and concise laws stated in a mathematical way that talks about the relationships between just a handful of concepts. So we have force, mass, distance, and time. And it's become the prototype for other scientific theories. It's the thing that they try to be like. A very concise few concepts a lot of abstraction.

Now what did Newtonian mechanics replace? Well this is Aristotle. And so before Newton kind of formalized this, the most common form of physics was Aristotelian physics. And it had concepts like this. This is just a small excerpt of the total number of concepts. One concept is ideal speed. And that says that small things move faster than big things. And then there's natural place which says that rocks like to be close to the earth and then water likes to be on top of that and then air likes to be on top of that.

So if you move them they'll like naturally go back to their natural place. Then there's natural motion which is like when you're walking and you're your generating your own like smooth motion. Versus unnatural motion which is when you like get jostled and pushed by something acting on you and so that's unnatural to the object.
And this dominated for over a thousand years and people are always figuring out corner cases and stuff. But you see the the type of theory is different. This Aristotelian physics is like just pointing at stuff. It's like, oh! Small things move fast and rocks like to sink. This is pointing at phenomena and trying to come up with some explanation for that particular thing. Whereas in Newtonian, it comes up with a coherent theory with relationships among the entities that in some sense is it's like a whole view of the world. Instead of these pointing things.

So I'm trying to do something like this for the question of what is functional programming? If you google it today, you'll get a bunch of people explaining trying to explain what functional programming is. I feel like it's very much this kind of Aristotelian kind of thing where people are like: oh pure functions! Oh no side effects! Immutable values and they're just pointing. They're just pointing at little phenomena and not coming up with a coherent whole. And I think that's a detriment to the community because someone who doesn't know functional programming and is trying to learn about it, they are not gonna be convinced about using it by these definitions.
If you say there's no side effects, is people are like how do you get anything done? Like how do you send an email? How do you do network programming? So I'm I'm trying to develop a theory that answers these questions in the Newtonian style. So my talk is called A theory of Functional Programming. It's a theory. I'm trying to build this myself from, I don't know. I feel like I'm good at this kind of theory building. So that's why I'm taking a stab at it and no one has done it yet so why not me?
My name is Eric Normand. I run a company called PurelyFunctional.tv where I teach Clojure and functional programming. Mostly in written and video form. If you go to the web site within the Czech Republic, you'll get a discount code. So if you're visiting from out of the country, you might want to buy now. If you're here and if you're not visiting, if you live here, well sign up sooner rather than later. But the code will be good forever. Okay I'm also running a conference in New Orleans it's called ClojureSYNC. It's all about Clojure and you can get 10% off if you use that code. Also check out the website. We have great speakers. Alright! Let's get started.

So we all know that functional programming people will say it's a programming paradigm right? So they contrast it to imperative or object oriented. So I looked up the word paradigm like what does that actually mean, and I like this dictionary definition. I'll just go over some pieces of it so it's a philosophical or theoretical framework or worldview. So it's not saying you know, when you never start talking about worldviews, you got to bring in relativism. So it's not saying that this is a better worldview than others.
It's just a different perspective on a problem but it's a framework. It's a way of thinking. It's a set of tools that you have to solve a problem. It's got theories, laws, generalizations. What what are the pieces of the theory is laws and laws are relationships between generalizations concepts.
And it also contains the basic assumptions and the ways of thinking. So when we when I build a theory of this and I say we because I want everyone to participate it's I don't want it to just be mine it's got to be shared. So I'll say we. So when we'll building this, it has to take into account that it's not about any particular language or anything like that it's about the way we sink. Okay. Just to revisit, what is functional programming? This is the question we're trying to answer.

So I have some more specific goals for my theory. So I want to explain what it is that we actually do? So not from an academic perspective but from an industry perspective. What are we actually doing when we call it when we do what we call functional programming? And it has to be in terms that we can all understand even if we're not functional programmers.
We have to be able to use the concepts in it to explain why it has advantages over other paradigms. And especially the people who haven't done FP. That's one of the big problems is that, we have is that once you try it, you like it, but before you give it a chance, it might not make much sense. I want to avoid focusing on features. I feel like the functional world needs to be a little bit more unified in terms of you know, taking a stance on the important things instead of in fighting about you know, do you have pure functions and type-checking? That kind of thing.
So it's not, we're just gonna not talk about features at all in the theory. And then it has to give explanatory and predictive power. A good theory gives you something new that you didn't have before. Besides just pointing at stuff and explaining stuff you already have. You should be able to make draw conclusions from those things that you didn't draw before. And then finally, I feel like we should all agree. We should be able to come to a consensus about the terms we use and things like that.

Okay! Let's get into it. My theory. So the world is divided into three domains. Three types of things. Actions, data, and calculations. And we'll go over each of these.

So actions is, this is the dictionary definition. It's process of doing something, having some kind of effect, trying to achieve an aim. This is what we typically call effects or side effects. I use the term because well, we can talk about that on the couch. Why I'm avoiding this term but it affects this kind of a problematic term. So the way you could tell if something is an action is whether it matters when you call it or how many times you call it.
Okay. So have some examples. Sending a message over the network depending on the message. The content of the message when you send it could be important. It could come before or after another message. And so that order matters. What matters also sending multiple messages might have a different meaning from sending one. Writing to the file system if you read and write to the file on the disk. Other things can read it so it depends on if you wrote first or they read first. What effect the system is going to have? And then, of course, in memory, changing mutable state or even reading from it when you read from it is important.

Okay. Data. Data is very easy I think. It's so clear about what it's. What it is is factual information used as a basis for reasoning discussion or calculation. But some properties of data that make it fall into this category it's inert. It doesn't do anything. It just is what it is. It's another way of saying it's self identical. It's serializable very often, meaning you can come up with some linear encoding and bytes or in an ASCII or something to put it on the wire. But it requires interpretation because it's inert, it needs something to read it. Just like if you had some text it requires a person to read it to make any sense out of it. Data is the same. So these examples I'm sure are just super clear so I'm not even gonna read them.

And then, finally calculations. There wasn't a good definition for calculations. They would always say like calculations are the product of calculating and calculating is the act of making calculations. So I had some I had to use computation as my definition instead of calculation. But this is what where we put all the mathematical functions and the pure functions that we we think of in functional programming. The characteristic that makes them calculations is that, they're outside of time. Their mathematical relationship defined it. Doesn't matter when you run them doesn't even matter if you run them. The relationship will still hold.
There also preferentially transparent which is another way of saying you have you don't you can run it zero times and it has the same effect. You can replace the function call with its results at compile time. So you don't even have to run it at run time. Some examples list concatenation and summing numbers. I think this should all be clear. In fact, it might even be like too obvious. And you might be wondering why I'm up here talking about it and spending all your time talking about this. But if you google for a definition of functional programming, no one is saying this. So I feel like yes, it's obvious but someone has to write this down and someone has to do the SEO and get on the front page of Google. And so I'm just gonna do it.
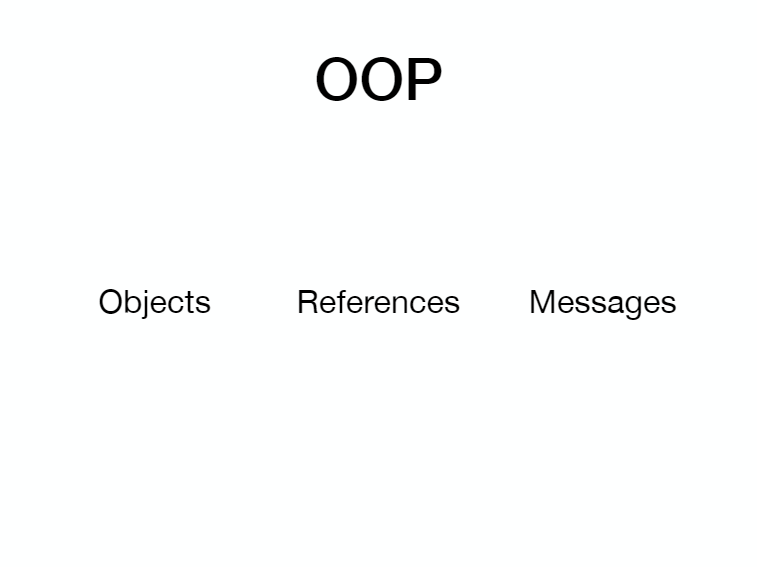
Another thing you might be wondering is, yes this is obvious, doesn't everyone do this? Doesn't everyone think about actions and calculations and data? So let's contrast, let's contrast this with object-oriented programming, and as a paradigm, how it divides up the world? So it also divides it into three categories of things. You've got objects references to those objects and messages that you can pass to any object that you have a reference to.
So notice there's no easy way to translate between object-oriented programming and functional programming. It's not that they're incompatible, they're just two different angles looking at the same problem. But they're both compatible. They're seeing the same thing but they're seeing different images right? Two-dimensional images because of the angle. So you could make data out of objects right? And you can say well this message is actually going to be pure. So it's a calculation and could do that but you'd have to do that yourself to make the translation. There's no simple way to translate between them.

Okay so just real quickly. Just to make sure this is super clear. How is it implemented in Haskell? How is functional programming in this theory implemented? So in Haskell, we have data types, built-in types, and we can define new types and that's the data. And then in the calculations are functions and in Haskell, all the functions are pure. So that's already done for us. And then the actions are this special type in the Haskell language called IO. So all of the actions go under that.

And then in Clojure, it's different because there's no type system and the semantics are a little different. So you have their built-in types and your collections of those types and stuff. That's the data. But then in Clojure, if you want calculations, you have to manually make your function pure because you could do impure stuff in your function. So if you keep your function pure, just by hand you can say that's a calculation and people do this. This is the idiomatic way of writing Clojure code. Say, oh! These are all pure functions. And then you have impure functions or your actions. So if you need to print to the screen or something you put it in an action. You put it in a function and you call it any prints of the screen.

Okay, so I hope that's all obvious because I'm gonna go further in. Because that was just laying the groundwork. Just the initial definitions. When we talk about functional programming, we often talk about first-class functions. So you can pass a function to another function. Or you can return a function from a function. But in functional programming, everything is first-class. Your data is first-class, your calculations are first-class, and your actions are first-class. So you can pass actions around. Compose them up just like you typically would think of posing up calculations. And I would argue that this is the minimal set feature set you need to do functional programming.
So let me give an example. In JavaScript, there are things that are not first-class. For instance, the plus operator is not first-class. You can't pass that as an argument to another function. but you can make something that does plus first-class you can make a function that does plus. That takes two arguments and wraps up that plus. And now you have something first-class that does the equivalent thing. So you could do a similar thing in in Java where you make a sort of a pure object that only does certain calculations in a pure way. And you can say those are my calculations. You can wrap it all up even if you don't have first-class functions.

Okay and this is also an important thing but it's it's kind of hard to explain. But the idea is that, these domains really are separate. There we are allowed to draw these lines. I want to make that clear. So in the data domain, we can make operations that compose two bits of data and get a new bit of data out right? So we can stay in this domain of data and not leave.
Just some examples. Addition of numbers, concatenation of lists or strings, and then we have calculations. You can do the same thing. You can take two calculations and make a new calculation. You don't have to leave the domain. Some examples of these kinds of composition. You have function composition which is kind of chaining the return of one to the argument of the next. And then juxtapose. Which is run both and put the results in a tuple.
And then, finally actions are also a domain that you can stay in. So you can have actions and compose them. Say in sequence or in parallel and they remain actions. Okay so I feel like that's an important idea that you can stay in each domain because what happens is, actions are contagious. And this gets that why we avoid side effects when we don't have to use them.

Actions combined with other things remain actions. So once you introduce side effects, everything that uses that thing it also could have a side effect. So just to make it like mathematically notation, you have a calculation and you combine it with an action, you're gonna get an action out. And if you have data and you combine it with an action, so you like hard code of value in the data, you're gonna get an action out.
So just as an example. If you had the function, it's a pure function square and you make a thing that takes the number squares it. And then prints it, that whole thing is also an action. Same if you do it the other way. You do read which is an action parse is just string to number let's say. So it's pure. But when you compose them, now you got an action. So the actions have not been properly quarantine.

Some things about calculations that are kind of corollaries to what we talked about. They're amenable to algebraic manipulation. Which means that you can do a lot of static analysis about them. And you can use the algebraic properties and the symbolic nature of our languages to do some cool stuff. There tor incomplete which is good but that introduces known problems like the halting problem. And then they're opaque. So you never know what a function is gonna do until you run it in general, you know you know some functions are easy and we'll, you can analyze some functions. But not all functions.

Okay. And then data. The nice thing about data is it's it is inert. And it's kind of self describing. It's just all out there like this is what I am. I'm just some data. And the problem with that is, it needs to be interpreted right? You can't just say: Okay, go run like you can a function. But it also means it can represent something else. It's self identical but it could also be the identity of another thing. Which that's that's interesting of itself. Also, due to data structure as a study. We know the Big O complexities of a lot of data structures. So it's got guaranteed like performance it. You know if you're using a map you know it's constant time reads stuff like that.

Okay now the generative part that I talked about. In the 30 minutes I have. I don't have time to go deep into this but this is something where we're actually able to generate potential refactorings of our code. Just by looking at the consequences of our definition. So if you take an action, that action might have been composed of an action and a calculation. So we can separate those two out. You can separate out all the pure stuff into its own thing and compose them back again later. And you'll have the same semantics of your code. Same with data. You could have a hard-coded value in there that you pull out as a parameter. And now you have an action and data separate. And the same goes for calculations. You can pull the data out you can also take two calculations and separate them into calculations.
But notice we can't do that with if we have a calculation, we know we're not going to get an action. There's no way to pull an action out of a calculation. It's pure you can't pull the impure part out. And that's interesting. We I mean we knew that but we didn't have a way to say that before.
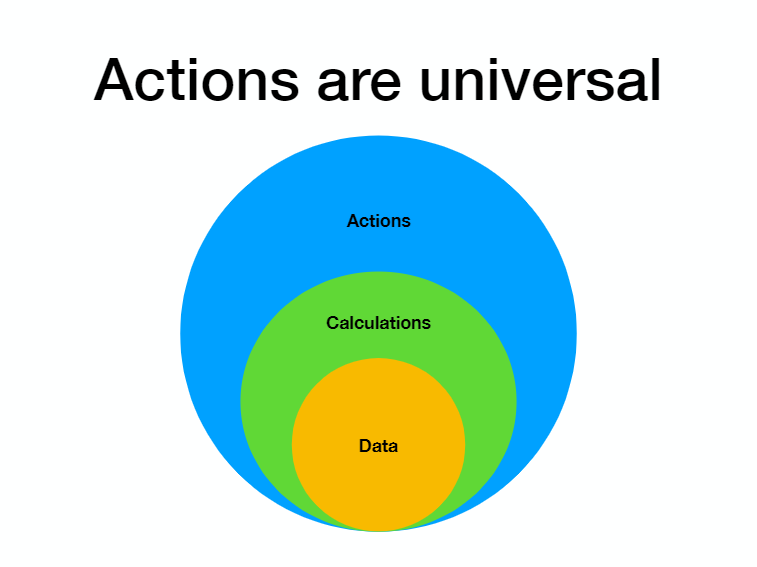
Okay. And now here's a question. Why is it that object-oriented programs and imperative programmers are a little afraid when you say we don't like actions? We don't like effects? Or side effects? And my answer to this is that, actions are the universal thing. Like you can do everything with actions. You can't do everything with data right? You can't just have a bunch of strings on your hard drive and like things are gonna run right? You need to have some code.
So we know through the lambda calculus that calculations themselves functions can represent data. So you can encode numbers and other data structures in functions and have a complete set of data that the kind of stuff all the types that we're used to. But what you can't get out of lambda calculus out of pure functions is, sending an email or launching a missile. Like you can never do that.
So you need actions. And actions are universal because you can just encode a turing machine that just mutates stuff and does the calculations and the data. So when an imperative programmer is like we don't really want so many actions. They're like but that's the that's the thing that lets you do everything else. And our job is to convince them that that that's true. But it is really nice that you get all these properties like algebraic reasoning when you separate out the calculations from the actions.

Aright. Another interesting idea is what counts as an action? So we said before that calculations are timeless. But actions are bound in time. So a pure function is a calculation. And reading and writing to disk is an action. So if I have a pure function, I would typically just put it in the calculations without thinking. But what if that function takes 24 hours to complete? All of a sudden when I run it, is kind of important right?
If I need the data now, I should have started yesterday. And I'm not gonna if I start now, I'm not gonna get the answer until tomorrow. That's bound in time for sure. Typically our functions take less than milliseconds to run. So we don't think about this. But there is some line somewhere that you have to decide for yourself. At what point does this function become if it runs long enough? At what point does it become an action right? So that's supposed to be animated but it just jumped.
Alright. Similarly, typically if I'm reading and writing to disk, I would put it in this column as an action. Except what if I do it to a temporary file that has a name that nothing can guess. And before it's before anything else can read it I'm already done and I deleted and clean it up. And I use it as a buffer. I just need a little bit more memory. And I just like do some calculations and store as like scratch paper right?
Well then you might say, that's actually a calculation. From the outside, it doesn't have any noticeable effects because we know that really, our computers are just doing actions right? That there every instruction in the machine code writes to a register or reads from memory somewhere some mutable thing. And we're the ones or our languages are the ones imposing the discipline of not trampling over each other's memory and and having a stack discipline. and things like that. So actually there is no calculation right? We have to make the calculation as functional programmers. So we get to choose where this line is.
So in Haskell, there's a thing called unsafe perform IO which lets you take an action something in IO and run it as if it were pure. So it the IO type is gone. So it's just a function now. So the type checker is happy. And as long as you are okay with the mutation and stuff happening, and you can treat it like a pure function.
Now in Clojure and in JavaScript, we play fast and loose all the time with this. So for instance, I'll write a pure function. And then I like what is this thing even doing? I put a print line in there and I see and so now it's impure. But like it's just for me the developer and then I deleted and so it didn't really matter.
Okay. More about the generative stuff. So there's enough study of functions and the algebraic manipulation of functions. That I feel like if someone's like: Well what about this functions? Can you tell me more about it? I can just say here's Lambda Calculus. You know you can read all about that.
But the interesting part that I feel like functional programmers are actually generating new stuff about is the actions. And people talk about we're avoiding actions. All that you know we're avoiding side-effects. And that's not really true. I think it's more fair to say that we're making actions safer right? And so if we take this idea that it's either how many times they run or when they run. We can actually divide up the space of actions into what's important.

So actions. If we say how many times they run? In this idea we can say that there's in general functions are they always matter. If they run zero times, it's different from one time. It's different from more times. This is certainly true for launching a missile. Launching zero missiles is way different from launching one missile. It's different from launching two missiles. And sending an email you know, if you don't send it, it's totally different from sending it ten times. Then we have the actions that are idempotent. So this means that zero is different. So sending it zero times is different from one time. But then, that second time it's the same. It doesn't matter if you sent it ten times versus one time. And we call that impotent.
So if you're gonna set the read flag on a on a file on your file system to true. If you set it again to true, it's the same. It hasn't changed anything. Same for like pressing an elevator button. You press it zero times, you know you're not gonna get picked up by the elevator. But you press it one time then you will second time it's not gonna have any effect. Then finally, we have actions that are totally free of side effects. So zero times, one time, more times. It's all the same. Still matters when they run. But it doesn't matter how many times. And so this is stuff like get requests. It has no external visible change to the world. Is that my signal? Yeah. Okay. I'm gonna continue.

Last slide. So then we have actions and when they run, and this I've divided into different semantics that we've come up with in the functional world. Like if you had a transactional read. It doesn't it still matters when they run. But you have a guarantee that you're never gonna read an inconsistent value. A value when but you know during a transaction, you'll always read either before or after. So even though you still matter when they run, like you you're guaranteed that it's at least consistent.
Transactional or serialized rights, so the same with writing. It doesn't matter. You can't guarantee any particular order of the rights. But we do know that it is in some order things don't happen at the same time. And then finally exactly once reads so you could have a queue that has tasks that you need to do. And you can guarantee that only one thread will pull that task off of the queue. The other ones are still waiting for their tasks. So you don't have it run twice. Because two threads got it. So those things help us reason about the actions. Okay my time is up I'm gonna be over here on the couches so when when you want to talk I'll be right there. Thank you very much!